Kurvendiskussion
Wenn man eine Kurvendiskussion für eine vorgegebene Funktion f(x) führen will,
so hat dies zum Ziel, gewisse Charakteristika des Graphen von f(x) herauszuarbeiten.
Diese sind vor allem folgende:
- Definitions- und Wertebereich
- Hoch-, Tief- und Wendepunkte
- Asymptoten und Polstellen
- Nullstellen
- Untersuchung auf Monotonie
- Symmetrien
Definitionsbereich
Der Definitionsbereich ist die Menge aller Werte, für die die vorgegebene Funktion f(x) definiert ist. Gesucht sind somit alle Werte, die man für x in f(x) einsetzen darf. Wir schreiben symbolisch Df für "Definitionsmenge der Funktion f".
In der Schule haben Sie außerdem das Symbol R für die "Menge der reellen Zahlen" kennen gelernt. In vielen Fällen ist die Definitionsmenge einer Funktion ganz R, d.h. man darf alle Zahlen für x einsetzen. In anderen Fällen gilt dies aber nicht, beispielsweise wenn Wurzen oder Logarithmen vorkommen oder wenn die Funktion einen Nenner hat. Falls eine Funktion ein Nenner hat, so müssen die Nullstellen des Nenners ausgeschlossen werden, da man durch Null nicht teilen darf. Falls eine Wurzel vorkommt, müssen alle Werte ausgeschlossen werden, die zu einer negativen Wurzel führen.
Beispiele
1) f(x)=x·ln(x) ⇒ Df=R+ (Menge der positiv reelen Zahlen).
2)
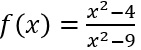⇒ Df=R\{3;-3}.3)
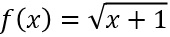⇒ Df=[-1;∞).Wertebereich
Der Wertebereich einer Funktion f(x) ist die Menge aller Werte, die die Funktion annehmen kann. Wir schreiben symbolisch Wf für "Wertebereich der Funktion f".
Beispiele
1) f(x)=ln(x) ⇒ Wf=R.
2) f(x)=sin(x) ⇒ Wf=[-1;1].
3) f(x)=ex ⇒ Wf=R+.
| Downloads |
PowerPoint